Sammendrag

Generaliseringen af ​​mindste kvadraters regression til komplekse værdiansatte variabler er ligetil, bestående primært af erstatning af matrixtransponer med konjugattransponer i de sædvanlige matrixformler. Et kompleks -værdig regression svarer dog til en kompliceret multivariat multipel regression, hvis løsning ville være meget sværere at opnå ved hjælp af standardmetoder (reel variabel). Når den komplekse værdi model er meningsfuld, anbefales det derfor stærkt at bruge kompleks aritmetik til at opnå en løsning. Dette svar inkluderer også nogle foreslåede måder til at vise dataene og præsentere diagnostiske plots af pasformen.

For at gøre det nemmere, lad os diskutere tilfældet med almindelig (univariat) regression, som kan skrives

$$ z_j = \ beta_0 + \ beta_1 w_j + \ varepsilon_j. $$

Jeg har lov til at navngive den uafhængige variabel $ W $ og den afhængige variabel $ Z $, som er konventionelle (se f.eks. Lars Ahlfors, Kompleks analyse ). Alt, hvad der følger, er ligetil at udvide til multipel regressionsindstilling.

Fortolkning

Denne model har en let visualiseret geometrisk fortolkning: multiplikation med $ \ beta_1 $ vil omskalere $ w_j $ ved modulus af $ \ beta_1 $ og drej det omkring oprindelsen ved argumentet $ $ beta_1 $. Efterfølgende oversætter tilføjelsen af ​​$ \ beta_0 $ resultatet med dette beløb. Effekten af ​​$ \ varepsilon_j $ er at "jittere" den oversættelse lidt. Således er regression af $ z_j $ på $ w_j $ på denne måde et forsøg på at forstå samlingen af ​​2D-punkter $ (z_j) $ som stammer fra en konstellation af 2D-punkter $ (w_j) $ via en sådan transformation, der giver mulighed for nogle fejl i processen. Dette er illustreret nedenfor med figuren med titlen "Fit as a Transformation."

Bemærk, at omskalering og rotation ikke bare er nogen lineær transformation af planet: de udelukker f.eks. skæve transformationer. Således er denne model ikke den samme som en bivariat multipel regression med fire parametre.

Almindelige mindste kvadrater

For at forbinde den komplekse sag med den virkelige sag, lad os skrive

$ z_j = x_j + i y_j $ for værdierne for den afhængige variabel og

$ w_j = u_j + i v_j $ for værdierne for den uafhængige variabel.

Desuden skal parametrene skrives

$ \ beta_0 = \ gamma_0 + i \ delta_0 $ og $ \ beta_1 = \ gamma_1 + i \ delta_1 $.

Hver af de nye termer, der introduceres, er naturligvis ægte, og $ i ^ 2 = -1 $ er imaginær, mens $ j = 1, 2, \ ldots, n $ indekserer dataene.

OLS finder $ \ hat \ beta_0 $ og $ \ hat \ beta_1 $, der minimerer summen af ​​kvadrater af afvigelser,

$$ \ sum_ {j = 1} ^ n || z_j - \ venstre (\ hat \ beta_0 + \ hat \ beta_1 w_j \ højre) || ^ 2 = \ sum_ {j = 1} ^ n \ venstre (\ bar z_j - \ venstre (\ bar {\ hat \ beta_0} + \ bar {\ hat \ beta_1} \ bar w_j \ højre) \ højre) \ venstre (z_j - \ venstre (\ hat \ beta_0 + \ hat \ beta_1 w_j \ højre) \ højre). $$

Formelt er dette identisk med den sædvanlige matrixformulering: sammenlign det med $ \ left (z - X \ beta \ right) '\ left (z - X \ beta \ right). $ Den eneste forskel, vi finder er, at transponere af designmatrixen $ X '$ erstattes af konjugat transponere $ X ^ * = \ bar X' $. Derfor er den formelle matrixløsning

$$ \ hat \ beta = \ left (X ^ * X \ right) ^ {- 1} X ^ * z. $$

På samme tid, for at se hvad der kan opnås ved at kaste dette til et rent virkeligt variabelt problem, kan vi skrive OLS-målet ud med hensyn til de reelle komponenter:

$ $ \ sum_ {j = 1} ^ n \ venstre (x_j- \ gamma_0- \ gamma_1u_j + \ delta_1v_j \ højre) ^ 2 + \ sum_ {j = 1} ^ n \ venstre (y_j- \ delta_0- \ delta_1u_j- \ gamma_1v_j \ højre) ^ 2. $$

Dette repræsenterer åbenbart to sammenkædede virkelige regressioner: den ene regresserer $ x $ på $ u $ og $ v $, den anden regresserer $ y $ på $ u $ og $ v $; og vi kræver, at $ v $ -koefficienten for $ x $ er den negative af $ u $ -koefficienten for $ y $ og $ u $ -koefficienten for $ x $ svarer til $ v $ -koefficienten for $ y $. Desuden, fordi total firkanterne for rester fra de to regressioner skal minimeres, vil det normalt ikke være tilfældet, at et sæt koefficienter giver det bedste skøn for $ x $ eller $ y $ alene. Dette bekræftes i nedenstående eksempel, som udfører de to reelle regressioner hver for sig og sammenligner deres løsninger med den komplekse regression.

Denne analyse gør det klart, at omskrivning af den komplekse regression med hensyn til de reelle dele (1 ) komplicerer formlerne, (2) tilslører den enkle geometriske fortolkning, og (3) vil kræve en generaliseret multivariat multipel regression (med ikke-trivielle korrelationer blandt variablerne) for at løse. Vi kan gøre det bedre.

Eksempel

Som et eksempel tager jeg et gitter med $ w $ -værdier på integrale punkter nær oprindelsen i det komplekse plan. Til de transformerede værdier tilføjes $ w \ beta $ med fejl, der har en bivariat Gaussisk fordeling: især er de reelle og imaginære dele af fejlene ikke uafhængige.

Det er vanskeligt at tegne den sædvanlige spredningsdiagram af $ (w_j, z_j) $ for komplekse variabler, fordi den vil bestå af punkter i fire dimensioner. I stedet kan vi se scatterplot-matrixen for deres virkelige og imaginære dele.

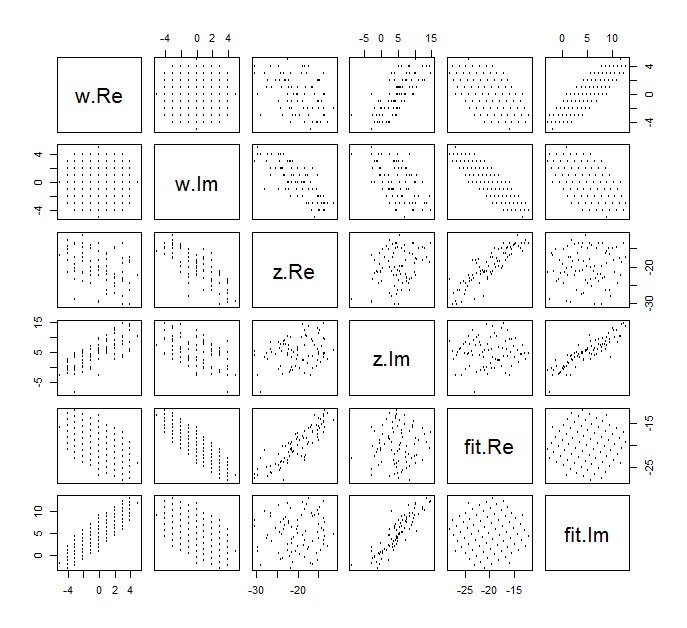
Ignorer pasformen for nu og se på de øverste fire rækker og fire venstre kolonner: disse vises dataene. Det cirkulære gitter på $ w $ er tydeligt øverst til venstre; den har $ 81 $ point. Spredningsdiagrammerne for komponenterne i $ w $ mod komponenterne i $ z $ viser klare sammenhænge. Tre af dem har negative sammenhænge; kun $ y $ (den imaginære del af $ z $) og $ u $ (den reelle del af $ w $) er positivt korreleret.

For disse data er den sande værdi af $ \ beta $ $ (- 20 + 5i, -3/4 + 3/4 \ sqrt {3} i) $. Det repræsenterer en udvidelse med $ 3/2 $ og en rotation mod uret på 120 grader efterfulgt af oversættelse af $ 20 $ enheder til venstre og $ 5 $ enheder op. Jeg beregner tre tilpasninger: den komplekse mindste firkantede løsning og to OLS-løsninger til $ (x_j) $ og $ (y_j) $ separat, til sammenligning.

  Fit Intercept Slope (s) True -20 + 5 i -0,75 + 1,30 iComplex -20,02 + 5,01 i -0,83 + 1,38 iReal kun -20,02 -0,75, -1,46 Kun imaginært 5,01 1,30, -0,92  

Det vil altid være tilfældet at den virkelige eneste aflytning er enig med den reelle del af den komplekse aflytning og den imaginære eneste aflytning er enig med den imaginære del af den komplekse aflytning. Det er imidlertid tydeligt, at de eneste reelle og imaginære skråninger hverken er enige med de komplekse hældningskoefficienter eller med hinanden, nøjagtigt som forudsagt.

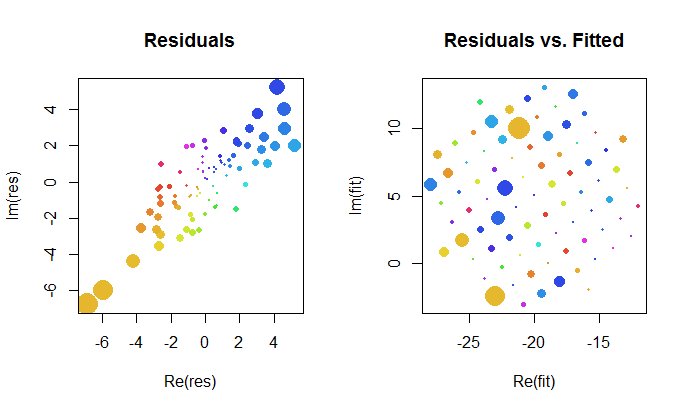
Lad os se nærmere på resultaterne af komplekset passe. For det første giver et plot af restprodukter os en indikation af deres bivariate Gaussiske fordeling. (Den underliggende fordeling har marginale standardafvigelser på $ 2 $ og en korrelation på $ 0,8 $.) Derefter kan vi plotte størrelsen på restprodukterne (repræsenteret af størrelsen på de cirkulære symboler) og deres argumenter (repræsenteret af farver nøjagtigt som i den første plot) mod de monterede værdier: dette plot skal se ud som en tilfældig fordeling af størrelser og farver, som det gør.

Endelig kan vi skildre pasformen på flere måder. Tilpasningen dukkede op i de sidste rækker og kolonner i scatterplot-matrixen ( q.v. ) og kan være værd at se nærmere på dette punkt. Nedenfor til venstre er pasningerne tegnet som åbne blå cirkler, og pile (der repræsenterer resterne) forbinder dem til dataene, vist som faste røde cirkler. Til højre vises $ (w_j) $ som åbne sorte cirkler udfyldt med farver svarende til deres argumenter; disse er forbundet med pile til de tilsvarende værdier på $ (z_j) $. Husk at hver pil repræsenterer en udvidelse med $ 3/2 $ omkring oprindelsen, rotation med $ 120 $ grader og oversættelse med $ (- 20, 5) $ plus den bivariate guassiske fejl.

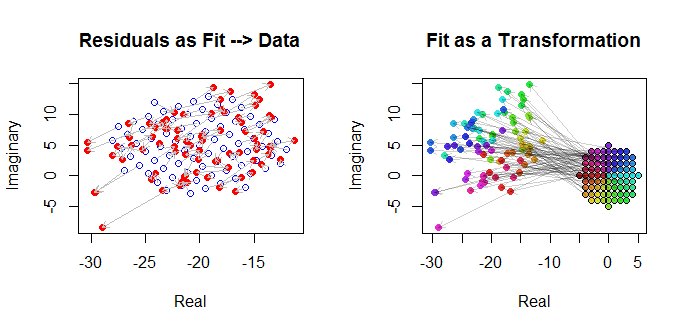
Disse resultater, plottene og de diagnostiske plotter antyder alle, at den komplekse regressionsformel fungerer korrekt og opnår noget andet end separate lineære regressioner af de reelle og imaginære dele af variablerne.

Kode

R -koden til oprettelse af data, tilpasninger og plot vises nedenfor. Bemærk, at den aktuelle løsning af $ \ hat \ beta $ opnås i en enkelt kodelinje. Yderligere arbejde - men ikke for meget af det - ville være nødvendigt for at opnå den sædvanlige mindste kvadraters output: varians-kovariansmatrixen for pasformen, standardfejl, p-værdier osv.

  ## Syntetiser data. # (1) den uafhængige variabel` w`. # w.max <- 5 # Max omfang af de uafhængige værdier w <- expand.grid (seq (- w.max, w.max), seq (-w.max, w.max)) w <- kompleks (real = w [[1]], imaginær = w [[2]]) w <- w [Mod (w) < = w.max] n <- længde (w) ## (2) den afhængige variabel `z`. # beta <- c (-20 + 5i, kompleks (argument = 2 * pi / 3, modul = 3/2)) sigma <- 2; rho <- 0,8 # Parametre for fejlfordelingsbiblioteket (MASS) # mvrnormset.seed (17) e <- mvrnorm (n, c (0,0), matrix (c (1, rho, rho, 1) * sigma ^ 2 , 2)) e <- kompleks (real = e [, 1], imaginær = e [, 2])
z <- as.vector ((X <- cbind (rep (1, n), w))% *% beta + e) ​​## Tilpas modellerne. # print (beta, cifre = 3) print (beta.hat <- løse (Conj (t (X))% *% X, Conj (t (X))% *% z), cifre = 3) print (beta.r <- coef (lm (Re (z) ~ Re (w) + Im (w))), cifre = 3) print (beta.i <- coef (lm (Im (z) ~ Re (w) + Im (w))), cifre = 3) ## Vis nogle diagnostik. # par (mfrow = c (1,2)) res <- as.vector (z - X% *% beta.hat) passer til <- z - ress <- sqrt (Re (middel (Conj (res)) * res))) col <- hsv ((Arg (res) / pi + 1) / 2, .8, .9) størrelse <- Mod (res) / splot (res, pch = 16, cex = størrelse, col = col, main = "Residuals") plot (Re (fit), Im (fit), pch = 16, cex = size, col = col, main = "Residuals vs. Fitted") plot (Re (c (z, fit)), Im (c (z, fit)), type = "n", main = "Rester som Fit --> Data", xlab = "Real", ylab = "Imaginary") punkter (Re (fit) , Im (fit), col = "Blå") punkter (Re (z), Im (z), pch = 16, col = "Red") pile (Re (fit), Im (fit), Re (z) , Im (z), col = "Grå", længde = 0,1) col.w <- hsv ( (Arg (w) / pi + 1) / 2, .8, .9) plot (Re (c (w, z)), Im (c (w, z)), type = "n", main = " Passer som en transformation ", xlab =" Real ", ylab =" Imaginary ") punkter (Re (w), Im (w), pch = 16, col = col.w) point (Re (w), Im (w )) punkter (Re (z), Im (z), pch = 16, col = col.w) pile (Re (w), Im (w), Re (z), Im (z), col = "# 00000030 ", længde = 0,1) ## Vis dataene. # Par (mfrow = c (1,1)) par (cbind (w.Re = Re (w), w.Im = Im (w), z.Re = Re (z), z.Im = Im (z), fit.Re = Re (fit), fit.Im = Im (fit)), cex = 1/2)  

Efter en god lang google sesh fandt jeg nogle relevante oplysninger om, hvordan problemet blev forstået på en alternativ måde. Det viser sig, at lignende problemer er noget almindelige i statistisk signalbehandling. I stedet for at starte med en Gaussisk sandsynlighed, der svarer til en lineær mindste firkant for ægte data, starter man med en:

http://en.wikipedia.org/wiki/Complex_normal_distribution

Specifikt, hvis du kan antage, at fordelingen af ​​din estimator $ \ hat {\ beta} $ er multivariat normal, så i tilfælde af komplekse data man ville bruge den komplekse normale. Beregningen af ​​covariansen for denne estimator er lidt anderledes og gives på wiki-siden.

Lærebogen af ​​Giri, Multivariate Statistical Analysis, dækker også dette.

Dette spørgsmål er kommet op igen på Mathematica StackExchange, og mit svar / udvidede kommentar der er, at @whubers fremragende svar skal følges.

Mit svar her er et forsøg på at udvide @whubers svar lidt ved at gøre fejlstrukturen lidt mere eksplicit. Den foreslåede estimator for mindste kvadrat er, hvad man ville bruge, hvis den bivariate fejlfordeling har en nul korrelation mellem de reelle og imaginære komponenter. (Men de genererede data har en fejlkorrelation på 0,8.)

Hvis man har adgang til et symbolsk algebra-program, kan noget af rodet ved at konstruere maksimale sandsynlighedsestimatorer for parametrene (både de "faste" effekter og kovariansstrukturen) elimineres. Nedenfor bruger jeg de samme data som i @whubers svar og konstruerer de maksimale sandsynlighedsestimater ved at antage $ \ rho = 0 $ og derefter ved at antage $ \ rho \ neq0 $ . Jeg har brugt Mathematica men jeg formoder, at ethvert andet symbolsk algebra-program kan gøre noget lignende. (Og jeg har først sendt et billede af koden og output efterfulgt af den faktiske kode i et tillæg, da jeg ikke kan få Mathematica -koden til at se ud som den skal ved blot at bruge tekst.)

Nu for de maksimale sandsynlighedsestimater forudsat $ \ rho = 0 $ ...

Vi ser, at de maksimale sandsynlighedsestimater, der antager, at $ \ rho = 0 $ matcher perfekt med de samlede estimater for mindste kvadrater.

Lad nu dataene bestemme et skøn for $ \ rho $ :

Vi ser, at $ \ gamma_0 $ og $ \ delta_0 $ er stort set identiske, uanset om vi tillad estimering af $ \ rho $ . Men $ \ gamma_1 $ er meget tættere på den værdi, der genererede dataene (selvom slutninger med en stikprøvestørrelse på 1 ikke skal betragtes som endelige for at sige det mildt) og loggen over sandsynligheden er meget højere.

Mit pointe i alt dette er, at modellen, der passer, skal gøres helt eksplicit, og at symbolske algebra-programmer kan hjælpe med at lindre rodet. (Og selvfølgelig antager de maksimale sandsynlighedsestimatorer en bivariat normalfordeling, som estimaterne med mindst kvadrat ikke antager.)

Appendiks: Den fulde Mathematica kode

Mens @whuber har et smukt illustreret og godt forklaret svar, synes jeg det er en forenklet model, der savner noget af det komplekse rums kraft.

Lineær mindste kvadraters regression på real svarer til følgende model med input $ w $, parametre $ \ beta $ og mål $ x $:

$$ z = \ beta_0 + \ beta_1 w + \ epsilon $$

hvor $ \ epsilon $ er normalt fordelt med nul middelværdi og en vis (typisk konstant) varians.

Jeg foreslår, at kompleks lineær regression defineres som følger:

$$ z = \ beta_0 + \ beta_1 w + \ beta_2 \ overline w + \ epsilon $$

Der er to store forskelle.

Først er der en ekstra grad af frihed $ \ beta_2 $, der tillader fasefølsomhed. Du vil måske ikke have det, men det kan du nemt have.

For det andet er $ \ epsilon $ en kompleks normalfordeling med middelværdi nul og noget varians og "pseudovarians".

Når vi går tilbage til den virkelige model, kommer den almindelige mindste kvadrat-løsning ud og minimerer tabet, hvilket er den negative log-sandsynlighed. For en normalfordeling er dette parabolen:

$$ y = ax ^ 2 + cx + d. $$

hvor $ x = z - (\ beta_0 + \ beta_1 w) $, $ a $ er fast (typisk), $ c $ er nul pr. model, og $ d $ betyder ikke noget, da tabsfunktioner er invariant under konstant tilsætning.

Tilbage til den komplekse model er den negative log-sandsynlighed \ begin {align} y = a {| x |} ^ 2 + \ Re ({bx ^ 2 + cx}) + d. \ end {align}

$ c $ og $ d $ er nul som før. $ a $ er krumning og $ b $ er "pseudo-krumning". $ b $ fanger anisotrope komponenter. Hvis $ \ Re $-funktionen generer dig, er en tilsvarende måde at skrive dette på \ begin {align} {\ begin {bmatrix} x- \ mu \\ \ overline {x- \ mu} \ end {bmatrix}} ^ H \ begin {bmatrix} s & u \\ \ overline {u} & \ overline {s} \ end {bmatrix} ^ {- 1} \! \ begin {bmatrix} x- \ mu \\ \ overline {x- \ mu} \ end {bmatrix} + d \ end {align} for et andet sæt parametre $ s, u, \ mu, d $. Her er $ s $ variansen og $ u $ er pseudovariansen. $ \ mu $ er nul i henhold til vores model.

Her er et billede af en kompleks normalfordelings tæthed:

Bemærk, hvordan det er asymmetrisk.Uden parameteren $ b $ kan den ikke være asymmetrisk.

Dette komplicerer regressionen, selvom jeg er temmelig sikker på, at løsningen stadig er analytisk.Jeg løste det for tilfældet med et input, og jeg er glad for at transkribere min løsning her, men jeg har en fornemmelse af, at whuber måske løser den generelle sag.