Beklager, lidt nyt her, så undskyld mig, hvis dette ikke hjælper for meget.

Den amerikanske socialsikringsadministration registrerer fødsler og dødsfald og har deres oplysninger tilgængelige for køb (tilsyneladende til en voldsom pris): Her

Jeg fandt dog en kilde, der hævder at have købt den og tilbyder den gratis (samt at tilbyde data sorteret efter dato på webstedet ): Her

Jeg antager, at du bare kan bruge det som din prøve og gå gennem alle dataene med et script og finde ud af, hvor mange mennesker der faktisk dør på deres fødselsdag. Jeg ville selv gøre det, men jeg har 20 minutter tilbage at downloade (de er ca. 1,5 GB), så jeg prøver selv at vende tilbage til dig om statistikken, hvis jeg finder tid til at skrive et script op.

Naturligvis kan USA ikke repræsentere hele verdens befolkning, men det er en god start. Jeg antager, at du vil se en højere sats i dødsfald på fødselsdage på grund af "første verdens problemer", fordi vi bruger USA, og jeg tror, ​​at effekten ville være mindre synlig i hele verden ...

Opdatering - numre: D

Jeg har kørt gennem Social Security Death Master File fra den gratis kilde, så der er ingen måde at vide, om oplysningerne er gyldige. I betragtning af størrelsen, at de er ~ 3 gigabyte hver, og at der ikke er nogen grund til, at nogen spoofer denne slags filer ... Jeg antager, at de er gyldige.

Du kan se koden, der Jeg plejede at løbe igennem det her: http://pastebin.com/9wUFuvpN

Det er skrevet i C #, det læser gennem linjerne i dødsindekset en efter en og derefter analyserer datoen ved hjælp af regex. Jeg antog, at filen stort set var i dette format:

  `(Social Security Number) (First Name) (LastName) (Middle Name) (Some Letter) (MM-DD-YYYY of Death) (MM-DD-ÅÅÅÅ Fødsel) ` 

Jeg havde regex bare vælg den sidste del til fødsels- / dødsdatoer, kontroller om nogen af ​​felterne kun er 0 (hvilket jeg antager, at det betyder, at socialsikring ikke kunne få en gyldig måned / dato for posten), og kassér 0'erne. Derefter kontrolleres det, om fødselsdagen og fødselsmåneden matcher dødsdagen / dødsmåneden og tilføjer det til den døde på fødselsdagstælling. Det tilføjer alle poster, der ikke er 0 til antallet af dødsfald.

Det viser resultaterne i dette format:

Dødsfald på fødselsdagen / Totalt antal dødsfald, der er set igennem - Folk med et 0 i en hvilken som helst af deres rekord

Det er dejligt, hvis nogen kunne dobbelttjekke den kode, da jeg har fundet en hel del fejl, jeg har lavet før, og kun kunne fortælle fordi mine resultater ikke gav nogen statistisk mening.

Her er konsoludgangen: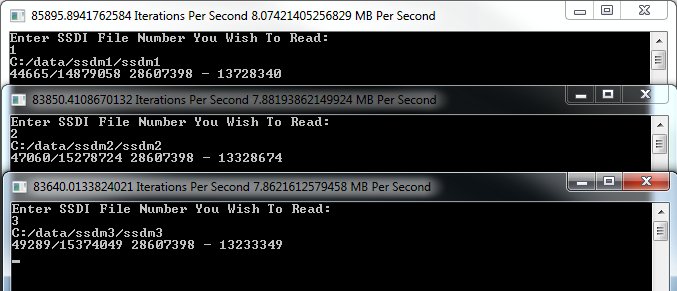

Gør noget matematik ...

• Fil 1 havde 44665 Dødsfald på en fødselsdag ud af 14879058 Dødsfald i alt
• Fil 2 havde 47060 Dødsfald på en fødselsdag ud af 15278724 Dødsfald i alt
• Fil 3 havde 49289 Dødsfald på en fødselsdag ud af 15374049 Dødsfald i alt
• I alt har vi 141014 Dødsfald på en fødselsdag ud af 45531831.

Så vi har ~ 0,3097% chance for at dø på en fødselsdag, mens vi er statistisk (1 / 365) ville få os til at tro, at der kun er ~ 0,27397% chance for at dø på en fødselsdag. Det er faktisk en stigning på 13% i risikoen for død på en fødselsdag fra 1/365. Selvfølgelig er denne prøve kun for amerikanere og har kun 45 millioner poster, jeg er sikker på, at organisationer, der oprindeligt offentliggjorde deres papir, havde adgang til meget mere pålidelige og større dødsindekser. Jeg tror dog, at det faktisk er gyldigt, at dødsfald på en fødselsdag er mere sandsynlige end døden på nogen anden dag.

Her er en tidsartikel, der citerer spring i årsager til død på fødselsdage: Artikel

Rediger 2: @cbeleites påpegede, at jeg glemte at redegøre for dødsfald samme dag, hvilket ville være en enorm faktor i at øge dødsfaldene på fødselsdage. Strengt taget er mine data stadig gyldige, men jeg kastede ikke ud, hvis en person døde samme dag, de blev født. Det er interessant, at mine resultater ikke blev påvirket for stærkt af denne fejl, så det ser ud til, at disse poster ikke inkluderer død den første dag. Jeg vil se nærmere på det senere. Jeg tænker, at der ville være meget interessante statistikker, jeg kan se efter, såsom død på månedens dage og lave et varmekort af en slags. Jeg vil sandsynligvis prøve at gøre det engang ...

Vi kan være endnu mere præcise end @Mike Shis data: den farligste af alle fødselsdage er den allerførste.

Dødeligheden på 1. dag rapporteret der er omkring 0,2% for industrialiserede lande og 0,8% gennemsnit for alle lande. Hvilket betyder, at risikoen for at dø på fødselsdagen er mindst lige så høj som risikoen for at dø nogen af de følgende fødselsdage *.

* Jeg synes, det er en sikker antagelse, at dødsfald på 1. dag ikke fremgår af @Mark Shis fil, da USAs første dags dødelighed rapporteres at være 0,3% ( anden kilde: 0,26%). Hvilket er næsten den samlede dødsrate i fødselsdagen i socialsikringsfilen. Så enten babyer, der dør på fødselsdagen, får ikke et personnummer, eller at dø på en fødselsdag> 1 år er ekstremt usandsynligt.

sidebemærkning:
Der er andre dage, såsom Chirstmas og nytårsaften, som det også vides at have en dødelighed højere end gennemsnittet.

Her er et argument for, at sandsynligheden for død på fødselsdagen kan være højere end andre dage: Fødselsdage er følelsesladede dage. Mere end folk har en tendens til at fejre det på en eller anden måde .. Så der er et overskud af faktorer (i forhold til personens sædvanlige livsstil), der øger biologisk stress (overskydende følelser, overdreven drikke, overdreven spisning, overskydende dans, overskydende banjee-spring osv.). Statistisk set øger denne situation chancerne for at dø på en fødselsdag, da den intensiverer eventuelle sundhedsmæssige problemer, en person måtte have, eller fordi den udsætter personen for situationer og risici, som personen er uerfaren for.

Sandsynligheden for, at en nyfødt dør inden for et år, findes i livstabellerne. For eksempel kan du tjekke de periodiske livstabeller og se i kolonnen $ q_x $ for $ x = 0 $ i den menneskelige dødelighedsdatabase. Dette er ikke nøjagtigt det, du ønsker, men giver dig en idé.

Ud over de andre fremragende svar, men der er et punkt, ingen af ​​dem diskuteres: Fødselsdage er ikke ensartet fordelt over året, og heller ikke dødsdage. Det sammensværger sådan, at den "statistiske" sandsynlighed er not 1/365. For at få et indtryk af denne effekt, lad os først antage, at de begge er næsten ensartede, kun 29. februar har sandsynligheden 1/4 af de andre. Det giver $$ 365 p + \ frac14 p = 1 $$ så $ p = 0.002737851 $ . Det fører til sandsynligheden for fødsel og død samme dag lig $ 356 \ cdot p ^ 2 + (p / 4) ^ 2 = 0.002736445 > 0.00273224 = \ frac1 {366} $ span> som er den mindst mulige værdi (med 366 dage).

Med lidt mere generelitet, lad $ p_i, i = 1, \ dotsc, n $ være fødselsdagssandsynlighederne, og $ q_i, i = 1, \ dotsc, n $ sandsynligheden for dødsdagen i et år med $ n $ dage. Så hvis fødselsdag og dødsdag for en person er statistisk uafhængig, finder vi det $$ \ DeclareMathOperator {\ P} {\ mathbb {P}} \ P (\ text {Fødsel og død samme dag}) = \ sum_ {i = 1} ^ n p_i q_i $$ så hvis $ p_i = q_i $ så er det $ \ sum_i p_i ^ 2 $ . Det er en mængde kendt (i biologi) som Simpsons-indeks for (bio) mangfoldighed. Dens inverse kunne derefter tages som "effektivt antal dage (om et år)"! Minimumsværdien af ​​ $ \ sum_i p_i ^ 2 $ er $ 1 / n $ . For at se det bruge konveksitet.

Men hvis vi antager, at $ p_i = q_i $ er ret stræk, kan vi først se på nogle data, fødselsdagssandsynligheder for Norge beregnet ud fra data fra ssb.no:

Klart ikke ensartet, den høje outlier er 1. juli. Det er ikke rigtigt, det er forårsaget af indvandrere uden dokumenteret fødselsdag registreret den dato. Et maksimum om foråret, omkring begyndelsen af ​​april, et andet maksimum om efteråret i september. Simpson-indekset beregnet ud fra dette er $ 0,002750224 $ , og det omvendte er $ 363,6067 $ , så det "effektive antal fødselsdage "er omkring 363 og en halv, snarere tæt på 366. Så ikke-ensartetheden er måske ikke så vigtig. Det er sværere at finde data til dødsdagen, men jeg fandt papiret (på norsk) (dette er den norske medicinske forenings officielle tidsskrift), de rapporterer omkring 12% højere dødsrate om vinteren end i sommers. De rapporterer også en lidt øget risiko for død mandage! Faktisk viser internationale sammenligninger rapporteret af dette papir, at vinteroverskud er lavest i Skandinavien, i lande som Irland eller England handler det om dobbelt. Det kan være overraskende, kan det have at gøre med os skandinaver, der har varmere og bedre isolerede huse?

Fra det kan vi rekonstruere en dødsdagfordeling. Jeg tager vinteren halvår som november-april. Så kan vi beregne $$ p_w = 1,12 p_s \\ (182 \ cdot 1.12 + 184) p_s = 1 $$ der fører til $ p_s = 0.002578383, p_w = 0.002887789 $ og til sidst $ \ sum_i p_i q_i = 0.00273151 $ , dens inverse, det "effektive antal dage" er 366,1, temmelig tæt på 366! Antikorrelationen ( $ \ rho (p_i, q_i) = - 0,06 $ ) synes at udligne nonuniformiteten på en sådan måde, at vi lige så godt kunne antage ensartethed (og lige fordeling til fødselsdag og dødsdag). Det er ret interessant.

REDIGER: Her er et offentliggjort papir om uensartethed i fødselsdagsproblemet.

1 ud af 365 ville være de rigtige odds, fordi du garanteret vil dø en dag ud af et 365 dages år ... Derfor er odds 1 ud af 365.