Spørgsmål:
Hvorfor er der kun $ n-1 $ hovedkomponenter til $ n $ data, hvis antallet af dimensioner er $ \ ge n $?
GrokingPCA
2014-11-10 01:22:36 UTC
view on stackexchange narkive permalink

I PCA, når antallet af dimensioner $ d $ er større end (eller endda lig med) antallet af prøver $ N $, hvorfor er det så, at du højst vil have $ N-1 $ ikke-nul egenvektorer? Med andre ord er rangeringen af ​​kovariansmatricen blandt $ d \ ge N $ dimensionerne $ N-1 $.

Eksempel: Dine prøver er vektoriserede billeder, som er af dimension $ d = 640 \ times480 = 307 \, 200 $, men du har kun $ N = 10 $ billeder.

Forestil dig $ N = 2 $ point i 2D eller i 3D.Hvad er dimensionaliteten af manifolden, som disse punkter optager?Svaret er $ N-1 = 1 $: to punkter ligger altid på en linje (og en linje er 1-dimensionel).Den nøjagtige dimension af rummet betyder ikke noget (så længe det er større end $ N $), dine point optager kun 1-dimensionelt underrum.Så variansen er kun "spredt" i dette underområde, dvs. langs 1 dimension.Dette forbliver sandt for enhver $ N $.
Jeg vil bare tilføje en ekstra præcision til @amoeba's-kommentaren.Oprindelsespunkt betyder også noget.Så hvis du har N = 2 + oprindelse, er antallet af dimensioner yderst 2 (ikke 1).Imidlertid centrerer vi normalt i PCA dataene, hvilket betyder, at vi lægger oprindelsen _indefra_ pladsen i dataskyen - så bliver en dimension opbrugt, og svaret bliver "N-1", som vist ved amøbe.
Det er det, der forvirrer mig.Det er ikke centreringen i sig selv, der ødelægger dimensionen, ikke?Hvis du har nøjagtige N-prøver og N-dimensioner, har du selv efter centrering stadig N-egenvektorer ..?
Hvorfor?Det er centrering, der ødelægger en dimension.Centrering (med aritmetisk middel) "flytter" oprindelsen fra "udefra" ind i rummet "spændt" af dataene.Med eksemplet N = 2.2 point + noget oprindelse spænder generelt over et plan.Når du centrerer disse data, placerer du oprindelsen på en lige linje halvvejs mellem de 2 punkter.Så dataene spænder nu kun over linjen.
Euclid vidste det allerede for 2300 år siden: to punkter bestemmer en linje, tre punkter bestemmer et plan.Generelt bestemmer $ N $ point et $ N-1 $ dimensionelt * euklidisk rum *.
To svar:
gung - Reinstate Monica
2014-11-10 09:56:00 UTC
view on stackexchange narkive permalink

Overvej hvad PCA gør. Simpelthen opretter PCA (som oftest kørt) et nyt koordinatsystem ved at:

  1. flytte oprindelsen til centret af dine data,
  2. klemmer og / eller strækker akser for at gøre dem ens i længden, og
  3. roterer dine akser til en ny retning.

(Se denne fremragende CV-tråd for flere detaljer: Fornuftig analyse af hovedkomponentanalyse, egenvektorer & egenværdier.) Det roterer dog ikke bare din akser på en gammel måde. Din nye $ X_1 $ (den første hovedkomponent) er orienteret i dine datas retning for maksimal variation. Den anden hovedkomponent er orienteret i retning af den næststørste mængde variation der er vinkelret på den første hovedkomponent . De resterende hovedkomponenter dannes ligeledes.

Med dette i tankerne, lad os undersøge @ amoebas eksempel. Her er en datamatrix med to punkter i et tredimensionelt rum:
$$ X = \ bigg [\ begin {array} {ccc} 1 &1 &1 \\ 2 &2 &2 \ end {array} \ bigg] $$ Lad os se disse punkter i et (pseudo) tredimensionelt spredningsdiagram:

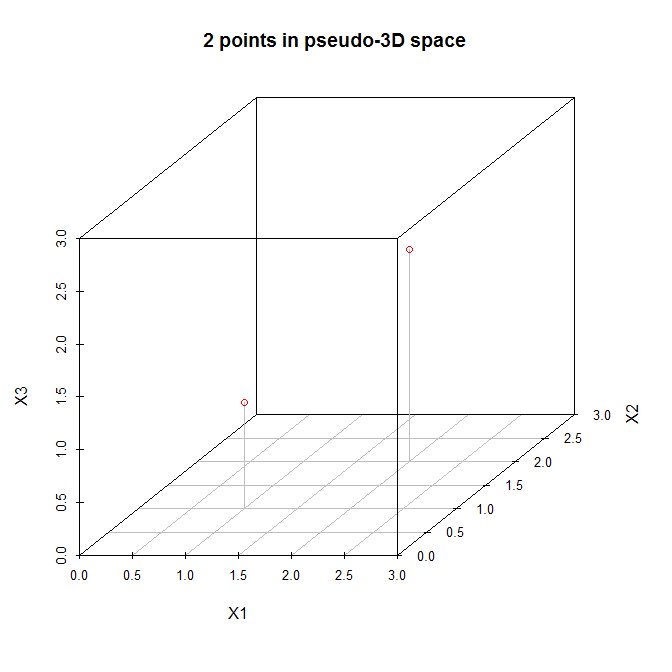
enter image description here

Så lad os følge de trin, der er anført ovenfor. (1) Oprindelsen af ​​det nye koordinatsystem ligger på $ (1,5, 1,5, 1,5) $. (2) Akserne er allerede lige. (3) Den første hovedkomponent vil gå diagonalt fra $ (0,0,0) $ til $ (3,3,3) $, hvilket er retningen for den største variation for disse data. Nu skal den anden hovedkomponent være vinkelret på den første og skulle gå i retning af den største tilbageværende variation. Men hvilken retning er det? Er det fra $ (0,0,3) $ til $ (3,3,0) $ eller fra $ (0,3,0) $ til $ (3,0,3) $ eller noget andet? Der er ingen resterende variation, så der kan ikke være flere hovedkomponenter .

Med $ N = 2 $ data kan vi (højst) passe $ N-1 = 1 $ hovedkomponenter.

Here
2020-05-31 08:10:21 UTC
view on stackexchange narkive permalink

Lad os sige, at vi har en matrix $ X = [x_1, x_2, \ cdots, x_n] $ , hvor hver $ x_i $ er en forstyrrelse (prøve) fra $ d $ dimension space, så $ X $ span> er en $ d $ af $ n $ matrix og $ d > n $ .

Hvis vi først centrerede datasættet, har vi $ \ sum \ limits_ {i = 1} ^ n x_i = 0 $ , hvilket betyder: $ x_1 = - \ sum \ limits_ {i = 2} ^ n x_i $ , så kolonnens rang på $ X \ leq n-1 $ , derefter $ rank (X) \ leq n-1 $ .

Vi ved, at $ rank (XX ^ T) = rank (X) \ leq n-1 $ , så $ XX ^ T $ har højst $ n-1 $ ikke-nul egenværdier.



ⓘ
Denne spørgsmål og svar blev automatisk oversat fra det engelske sprog.Det originale indhold er tilgængeligt på stackexchange, som vi takker for den cc by-sa 3.0-licens, den distribueres under.
Loading...